The very different subjects of Bayesian data analysis and foundation of Quantum Mechanics are related to each other by a common definition of probability based on the logic of true and false statements.
The foundation of Bayesian statistics is based on this operational definition of probability, where the different statements correspond to data or hypotheses (“the mass of Saturn is between 1/3512 and 1/3513 solar masses”, “The data represent a Lorentzian distribution”). From here, the rules to evaluate the probability distribution of the model parameter are deduced. At the same time, the probability to different models is deduced from the same set of data. The data analysis program Nested fit is based on this approach and is described in the next section.
The use of operational definition of probability based on logic can also be applied to Quantum Mechanics measurements opening new perspectives. In particular, classical and quantum probabilities can be derived from the same definition of the function probability, as discussed more extensively in the second section.
Nested_fit: a data analysis program based on Bayesian statistics
Team
- Permanent member: Martino Trassinelli
- PhD Student: Lune Maillard (2021-2024)Related projects
Related projects
-
Quantum NESTed sampling (QNEST) project for nuclear quantum effects in condense matter, in collaboration with the Low-Dimensional Oxides team
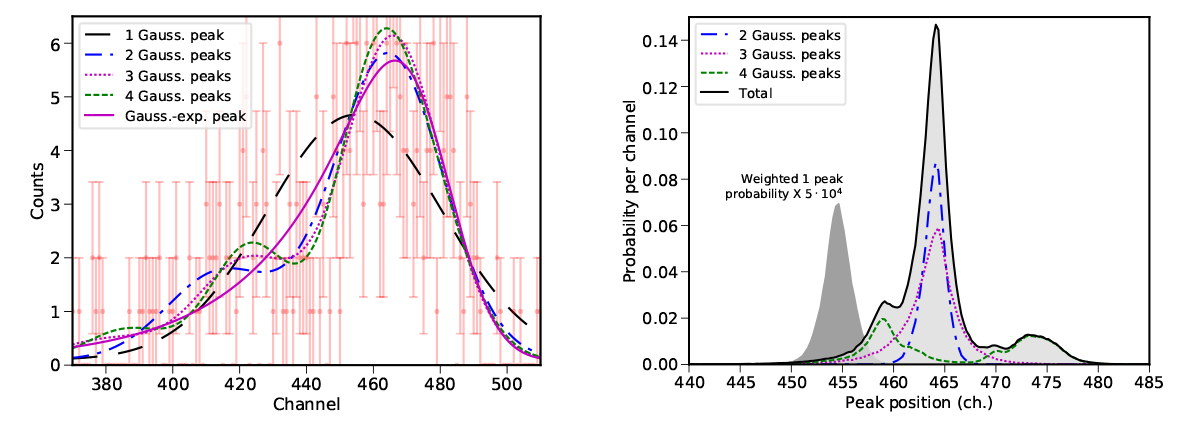
Figure 1: Left: Profile curves corresponding to the likelihood maxima of the models with different number of peaks. Right: Probability distribution of the main peak position from the single probabilities of the models.
Nested_fit is a program based on the Bayesian statistics specially developed for data analysis cases difficult to treat with standard approaches like minim chi-square. It is freely available here https://github.com/martinit18/nested_fit. In addition to the commonly fitting programs outputs like most probable parameter values and associated uncertainties, Nested_fit determines the complete probability distribution for each parameter, but also conjunct probabilities. More important, it provides the Bayesian evidence, a quantity required to compare different models (i.e. hypotheses, like the presence or not of additional peaks or the choice of the peak shape) related to the probability to the model itself. The model probabilities can be then used as weight to obtain a probability distribution of a common parameter from the different model assumptions (like the peak position in the figure) without need of choosing a particular model, an impossible task for standard statistical tools.
The evidence calculation is based on the nested algorithm (Sivia and J. Skilling, Data analysis: a Bayesian tutorial, 2006 Oxford University Press), which reduces a n-dimensional integral (the integral of the likelihood function in the n parameters space) to a one-dimensional integral. The Nested_fit code is written in Fortran90 with some Python complementary routines for visualizing the output results and for doing automatic analysis of data. It has been implemented for the analysis of spectra of different nature: X-ray emission spectra from heavy highly charged ions and pionic atoms, photoemission spectra from nanoparticles and nuclear decays.
A complete description of the program can be found in articles 1 and 2.
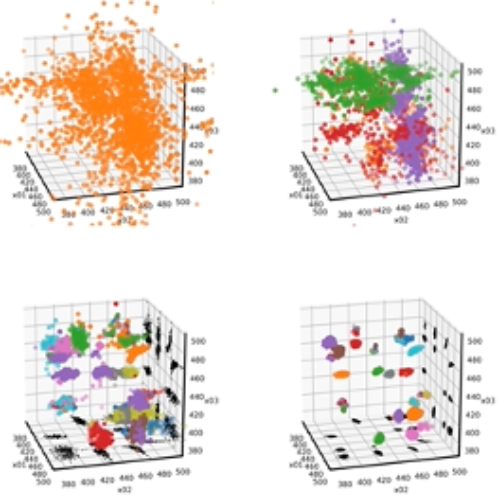
Figure 2: Cluster recognitions corresponding to the permutation of four Gaussian peaks (4!=24) for the data presented in the previous figure.
Nested sampling algorithm is based on an exploration using a dynamical set of sampling points that evolves to higher values of the sampled function. When several maxima of the likelihood function are present, this exploration can be a very difficult task. To overcome this issue, different machine learning methods are implemented, like cluster recognition and exploration methods. After a preliminary implementation [3], different methods have been tested for several scenarios and are now part of the latest version of the code [4].
In addition to several application for data analysis, at present Nested_fit program is also used to explore complex solid-state potential energy landscapes within the framework of the doctoral project “Quantum NESTed sampling” (QNEST) financed by the Sorbonne Center of Artificial Intelligence.
Quantum probability and foundations of quantum mechanics
Relational quantum mechanics and probability
The definition of the probability function for statements can easily be adapted to Relational Quantum Mechanics (RQM), a foundation for the Quantum Mechanics based on only three postulates. The first two are founded to the limited amount of information that can be extracted from interaction of different systems by questions (positive answer → logic statements). A third postulate was introduced to define the properties of the probability function in the original work (Rovelli, Int. J. Theor. Phys. 35, 1637 1996). From a rigorous definition of the conditional probability for the possible outcomes of different measurements, we demonstrate that the third postulate is unnecessary and the Born’s rule naturally emerges from the first two postulates by applying the Gleason’s theorem.
These results are presented in article 4.
Classical and quantum probabilities unified
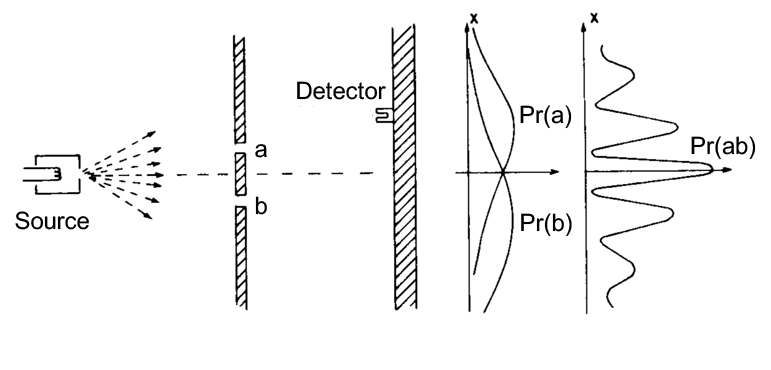
Figure 3: The space-time interference case of the Yong’s slits.
With a definition of the probability function by statements, we demonstrate that the probability function is uniquely defined for classical and quantum phenomena. Considering perfect projective measurements, the presence or not of interference terms is, in fact, related to the correct formulation of the conditional probability where distributive property on its argument cannot be taken for granted and where
(A OR B) AND C ≠ (A AND C) OR (B AND C).
The two probabilities P[(A OR B) AND C] and P[(A AND C) OR (B AND C)] correspond to the Born’s rule and the classical probability sum rule, respectively. In the case of the ideal Young’s slits experiment, the first expression gives rise to interferences, contrary to the second one.
This work has been extended from perfect to general measurements, where the detection itself is not represented by projectors in an Hilbert space but by positive operators (effects) in the context of positive-operator-valued measures (POVM). The frontier between the two different probability expressions, related to the intrinsic possibility to distinguish or not the particle path from intermediate measurement, can be here investigated varying the inaccuracy of the measurement.
In addition to space-like interference phenomena like the Young’s slits case, time-like interferences (where we deal with subsequent measurement with undefined order) can be studied with the same formalism. In time-like case, the “causal inequality” (Brukner, Quantum causality, Nat. Phys. 10, 259, 2014) can also be derived.
This work is presented in articles 5, 6.
Quantum time and the Wigner’s friend scenario
If everything is quantum, all the ingredients considered (measured system, measuring apparatus, observer, clock, etc.) can be described in a same Hilbert space, called kinematic Hilbert space. The dynamics of the system and its observation are now included in the global wave function, which extends in time and describes everything. In this framework, formulated for the first time by Page and Wootters in 1983, a clock is just an additional quantum system, consisting for example of a spin in precession, with the time defined by the orientation of the spin at the moment of its measurement.
Each measurement will consist of the measurement of the system studied plus a measurement of time from the “clock” system. The measurement pair corresponds to a operator in my kinematic space. The associated probability is simply deduced using Gleason’s theorem again. The expression of probability function, including the associated conditional probabilities resulting from an intermediate measure, is then well defined. This allows to describe also confusing cases like the Wigner’s friend scenario where one person observes another person and both measure apparently contradictory things (see figure). The obtained unambiguous expression of the probability for a particular a result underlines on the contrary the relative aspect of the measurements. Wigner sees his friend as being in a quantum superposition but also the friend sees Wigner in a superposition state. No paradoxical situation appears.
This work is presented in article 7.
Publications
- M. Trassinelli. Bayesian data analysis tools for atomic physics. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Elsevier, 2017, 408, pp.301-312. ⟨10.1016/j.nimb.2017.05.030⟩. ⟨hal-01405864v2⟩
- M. Trassinelli. The Nested_fit data analysis program. MDPI Proceedings, MDPI, 2019, 33 (1), pp.14. ⟨hal-02196171⟩
- M. Trassinelli, Pierre Ciccodicola. Mean shift cluster recognition method implementation in the nested sampling algorithm. Entropy, MDPI, 2020, 22 (2), pp.185. ⟨hal-02454806v2⟩
- L. Maillard, F. Finocchi, and M. Trassinelli, Assessing Search and Unsupervised Clustering Algorithms in Nested Sampling, Entropy, MDPI, 2023, 25 (2), pp.347.
⟨hal-03988205v1⟩ - M. Trassinelli. Relational Quantum Mechanics and Probability. Foundations of Physics, Springer Verlag, 2018, ⟨10.1007/s10701-018-0207-7⟩. ⟨hal-01723999v3⟩
- M. Trassinelli. Conditional probability and interferences in generalized measurements with or without definite causal order. Physical Review A, American Physical Society 2020, 102 (5), pp.052224. ⟨10.1103/PhysRevA.102.052224⟩ ⟨hal-02933221v2⟩
- M. Trassinelli, Conditional probabilities of measurements, quantum time, and the Wigner’s-friend case, Phys. Rev. A 105, 032213 (2022), ⟨10.1103/PhysRevA.105.032213 ⟩, ⟨hal-03179772v4⟩

