Les sujets que sont l’analyse des données bayésiennes et les fondations de la Mécanique Quantique peuvent paraitre très différents alors qu’ils sont liés par une définition commune de la probabilité basée sur la logique des propositions, vraies et fausses.
La fondation de la statistique bayésienne repose sur cette définition opérationnelle de la probabilité, où les différents propositions correspondent à des données ou des hypothèses (« la masse de Saturne est comprise entre 1/3512 et 1/3513 masses solaires », « Les données représentent une distribution lorentzienne »). De là, les règles pour évaluer la distribution de probabilité du paramètre du modèle sont déduites. Dans le même temps, la probabilité de différents modèles est déduite du même ensemble de données. Le programme d’analyse de données Nested_fit est basé sur cette approche et est décrit dans la section suivante.
L’utilisation de la définition opérationnelle de la probabilité basée sur la logique peut également s’appliquer aux mesures de Mécanique Quantique ouvrant de nouvelles perspectives. En particulier, les probabilités classiques et quantiques peuvent être dérivées à partir de la même définition de la fonction de probabilité, comme discuté plus en détail dans la deuxième section.
Nested_fit: un programme d’analyse de données basé sur les statistiques bayésiennes
Equipe
- Membre permanent : Martino Trassinelli
- Doctorante : Lune Maillard (2021-2024)
Projet associé
- Quantum NESTed sampling (QNEST) effet quantiques nucléaires dans la physique de la matière condensée, en collaboration avec le groupe Oxydes en basses dimensions
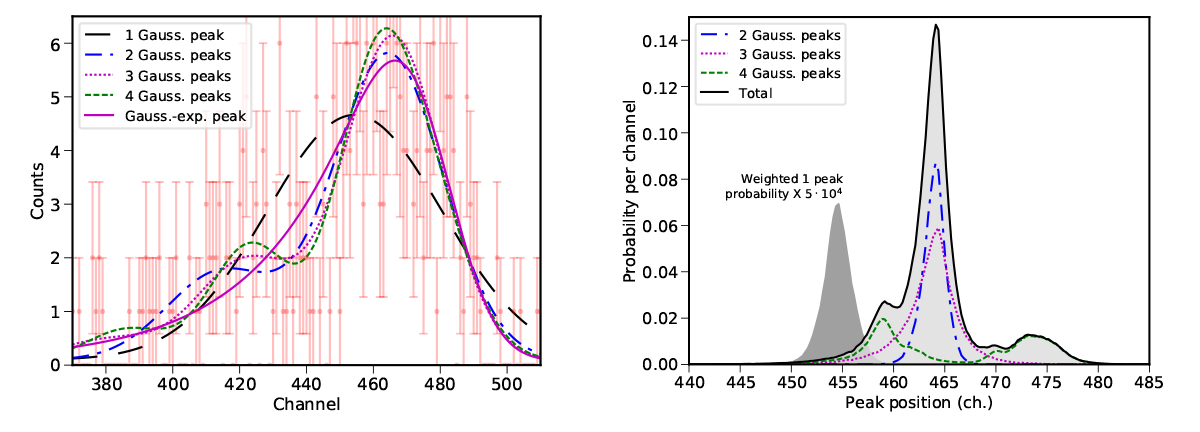
Figure 1 : Gauche: courbes de profil correspondant aux maxima de vraisemblance des modèles avec des nombres de pics différents. Droite: Distribution de probabilité de la position du pic principal à partir des probabilités de chaque modèle.
Nested_fit est un programme basé sur les statistiques bayésiennes spécialement développé pour l’analyse de données difficiles à traiter avec des méthodes traditionnelles comme le minimum du chi-carré. Il est disponible gratuitement sur le site https://github.com/martinit18/nested_fit. En plus des sorties standard des programmes d’analyses, comme les valeurs de paramètres les plus probables et les incertitudes associées, Nested_fit détermine la distribution complète de probabilité pour chaque paramètre, mais également les probabilités conjointes. Mais surtout, il fournit l’évidence Bayésienne, une quantité nécessaire pour comparer différents modèles (c’est-à-dire des hypothèses, comme la présence ou non de pics supplémentaires ou le choix de la forme du pic) liées à la probabilité au modèle lui-même. Les probabilités des modèles peuvent ensuite être utilisées comme poids pour obtenir des distributions de probabilité d’un paramètre commun à partir des différentes hypothèses du modèle (comme la position du pic sur la figure) sans avoir besoin de choisir un modèle particulier, chose impossible avec les approches classique de statistique.
Le calcul de l’évidence est basé sur l’algorithme « nested sampling » (Sivia et J. Skilling, Data analysis: a Bayesian tutorial, 2006 Oxford University Press), qui réduit une intégrale à n dimensions (l’intégrale de la fonction de vraisemblance dans le espace des n paramètres) à une intégrale unidimensionnelle. Le code Nested_fit est écrit en Fortran90 avec des routines complémentaires en Python pour visualiser les résultats de sortie et pour faire une analyse automatique sur les données. Il a été développé pour l’analyse de spectres de nature différente: spectres d’émission de rayons X à partir d’ions lourds hautement chargés et d’atomes pioniques, spectres de photoémission à partir de nanoparticules et désintégrations nucléaires.
Une description complète du programme peut être trouvée dans les articles 1 et 2.
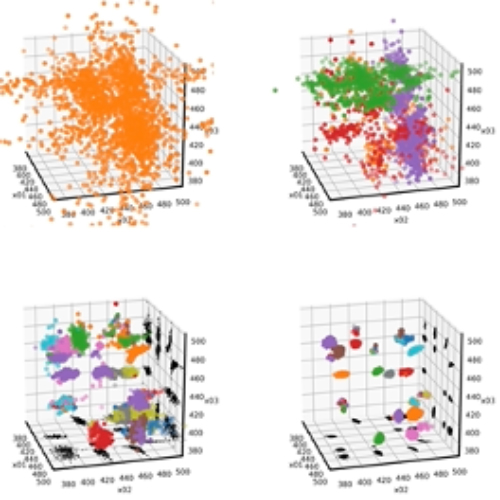
Figure 2 : Reconnaissances de clusters correspondant à la permutation de quatre pics gaussiens (4! = 24) pour les données présentées dans la figure précédente.
L’algorithme nested sampling est basé sur une exploration utilisant un ensemble dynamique de points d’échantillonnage qui évolue vers des valeurs plus élevées de la fonction échantillonnée. Lorsque plusieurs maxima de la fonction sont présents, cette exploration peut s’avérer très difficile. Pour surmonter ce problème, différentes méthodes d’apprentissage automatique (machine learning) sont mises en œuvre, plusieurs méthodes de partitionnement de données et des d’exploration. Après une mise en œuvre préliminaire [3], ces différentes méthodes ont été testées pour plusieurs scénarios et font désormais partie de la dernière version du code [4].
En plus de différentes applications d’analyse de données, le programme Nested_fit est actuellement aussi utilisé pour explorer des paysages complexes d’énergie potentielle de la matière condensée dans le cadre du projet doctoral « Quantum NESTed sampling » (QNEST) financé par le Sorbonne Center of Artificial Intelligence.
Probabilité quantique et fondement de la mécanique quantique
Mécanique quantique relationnelle et probabilité
La définition de la fonction de probabilité par des prépositions peut facilement s’adapter à la mécanique quantique relationnelle (RQM), une fondation de la Mécanique Quantique basée sur seulement trois postulats. Les deux premiers sont fondés sur la quantité limitée d’informations qui peuvent être extraite de l’interaction de différents systèmes par des questions (réponse positive → propositions logiques). Un troisième postulat a été introduit pour définir les propriétés de la fonction de probabilité dans le travail original (Rovelli, Int. J. Theor. Phys. 35, 1637 1996). À partir d’une définition rigoureuse de la probabilité conditionnelle pour les résultats possibles de différentes mesures, nous démontrons que le troisième postulat n’est pas nécessaire et que la règle de Born émerge naturellement des deux premiers postulats en appliquant le théorème de Gleason.
Ces résultats sont présentés dans l’article 5.
Unification des probabilités classiques et quantiques
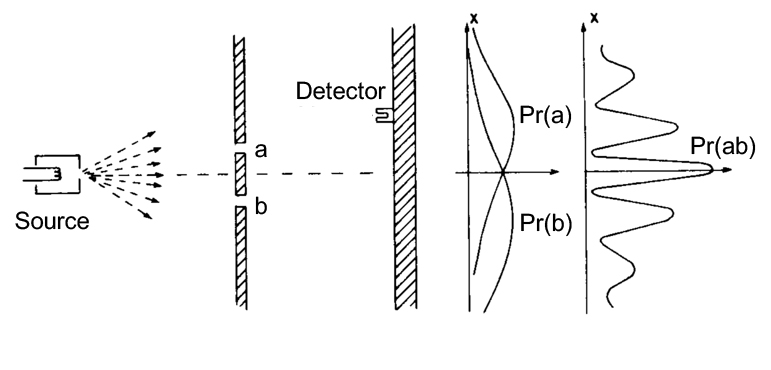
Figure 3 : Le cas d’interférence spatio-temporelle des fentes de Yong.
Avec une fonction de probabilité définie par proposition logiques, nous démontrons aussi que la fonction de probabilité est uniquement définie pour les phénomènes classiques et quantiques. En considérant des mesures projectives parfaites, la présence ou non de termes d’interférence est, en fait, liée à la formulation correcte de la probabilité conditionnelle où la propriété distributive de ses arguments ne peut pas être prise pour acquise et nous avons
(A OU B) ET C ≠ (A ET C) OU (B ET C).
Les deux probabilités P[(A OU B) ET C] et P[(A ET C) OU (B ET C)] correspondent respectivement à la règle de Born et à la règle classique de la somme des probabilités. Dans le cas de l’expérience idéale des fentes de Young, la première expression donne lieu à des interférences, contrairement à la seconde.
Ce travail a été étendu de mesures parfaites à des mesures plus générales, où la détection elle-même n’est pas représentée par des projecteurs dans l’espace de Hilbert mais par des opérateurs positifs (effets) dans le cadre de « mesures à valeur d’opérateur positive » (POVM). La frontière entre les deux expressions différentes de probabilité, liée à la possibilité intrinsèque de distinguer ou non le trajet des particules de la mesure intermédiaire, peut être ici étudiée en faisant varier l’imprécision de la mesure.
En plus aux phénomènes d’interférence de type spatial comme le cas des fentes de Young, les interférences de type temps (où une succession de mesures d’ordre indéterminé intervient) peuvent être étudiés avec le même formalisme. Dans le cas du temps, «l’inégalité causale» (Brukner, Quantum causality, Nat. Phys. 10, 259, 2014) peut également être dérivée.
Ce travail est présenté dans l’articles 5, 6.
Temps quantique et le cas de l’ami.e de Wigner
Si tout est quantique, tous les ingrédients considérés (système mesuré, appareil de mesure, observateur, horloge…) peuvent être décrits dans un même espace Hilbert, appelé espace de Hilbert cinématique, où la dynamique fait partie intégrante de la fonction d’onde globale qui s’étend dans le temps et qui décrit tout. Dans ce cadre, formulé pour la première fois par Page et Wootters en 1983, une horloge n’est qu’un système quantique comme les autres, consistant par exemple en un spin en précession avec l’heure définie par l’orientation du spin au moment de sa mesure.
Chaque mesure consistera en la mesure du système étudié plus une mesure du temps dans le système « horologe » qui correspondent à des operateurs dans mon espace cinématique. La probabilité associée est simplement déduite en utilisant le théorème de Gleason encore une fois. L’expression de cette probabilité, y compris les probabilités conditionnelles associées résultants d’une mesure intermédiaire, est alors bien définie. Ceci permet de décrire également des cas déroutants comme le scénario de l’ami.e de Wigner où une personne observe une autre personne et les deux mesurent des choses apparemment contradictoires (voir figure). L’expression non ambiguë de la probabilité d’obtenir un résultat souligne au contraire l’aspect relatif des mesures : Wigner voit son ami.e comme étant en superposition quantique mais aussi l’ami.e voit Wigner en état de superposition sans qu’aucune situation paradoxale n’apparaisse.
Ce travail est présenté dans l’article 7.
Publications
- M. Trassinelli. Bayesian data analysis tools for atomic physics. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Elsevier, 2017, 408, pp.301-312. ⟨10.1016/j.nimb.2017.05.030⟩. ⟨hal-01405864v2⟩
- M. Trassinelli. The Nested_fit data analysis program. MDPI Proceedings, MDPI, 2019, 33 (1), pp.14. ⟨hal-02196171⟩
- M. Trassinelli, Pierre Ciccodicola. Mean shift cluster recognition method implementation in the nested sampling algorithm. Entropy, MDPI, 2020, 22 (2), pp.185. ⟨hal-02454806v2⟩
- L. Maillard, F. Finocchi, and M. Trassinelli, Assessing Search and Unsupervised Clustering Algorithms in Nested Sampling, Entropy, MDPI, 2023, 25 (2), pp.347.
⟨hal-03988205v1⟩ - M. Trassinelli. Relational Quantum Mechanics and Probability. Foundations of Physics, Springer Verlag, 2018, ⟨10.1007/s10701-018-0207-7⟩. ⟨hal-01723999v3⟩
- M. Trassinelli. Conditional probability and interferences in generalized measurements with or without definite causal order. Physical Review A, American Physical Society 2020, 102 (5), pp.052224. ⟨10.1103/PhysRevA.102.052224⟩ ⟨hal-02933221v2⟩
- M. Trassinelli, Conditional probabilities of measurements, quantum time, and the Wigner’s-friend case, Phys. Rev. A 105, 032213 (2022), ⟨10.1103/PhysRevA.105.032213 ⟩, ⟨hal-03179772v4⟩

