List of members |
Facilities |
Internships and jobs |
PhD |
Publications |
News |
Team
- Permanent member: Olga Boyko
- Emeritus researcher: Bernard Bonello
Theorical aspects
Following the example of what happened about twenty years ago for photonic crystals, we are currently witnessing a certain effervescence around phononic crystals which, in principle, should present for acoustic waves the same properties of filtering, guiding, focusing, localization… as those observed for electromagnetic waves in photonic crystals.
Up to now, the vast majority of the works devoted to these systems concern the propagation of elastic volume waves in periodic structures where one of the constituents is a fluid (air in general). Transverse displacements are therefore never taken into consideration. It is only recently that surface waves have received special attention. An important part of our activity concerns the calculation of dispersion curves of phononic systems close to those we study experimentally (see below). These are what we could call “phononic films”, i.e. structures constituted by periodic inclusions of square symmetry of a material A, in a thin film of a material B, itself deposited on the surface of a semi-infinite homogeneous substrate of a material C.
If the thickness of the film is less than the repetition distance of the inclusions, the elastic wave propagates partly in the film and partly in the substrate and there is therefore a priori no evidence that a band gap appears for the surface wave. Nevertheless, we have shown that a band gap and aliasing for the surface mode appear at the X edge of the mini Brillouin zone for the phononic thin film configuration on a homogeneous semi-infinite substrate (Figure 1). The gap extends partially in the XM part of the Brillouin zone.

Figure 1: dispersion curves in the GX direction, for a phononic film made of cylindrical iron inclusions in a thin copper film, deposited on a silicon substrate. The filling ratio is f = 0.564. The pitch of the square lattice is 2 times the thickness of the film. Tlay, Tsub and Lsub refer respectively to the transverse modes in the film, transverse in the substrate and longitudinal in the substrate. The insert is a magnification highlighting the band gap and the folding of the Rayleigh mode at the zone edge.
We are also interested in a configuration in which the homogeneous substrate has a finite thickness. The system is then a plate on which the phononic film is deposited. In this case, there is a coupling between the acoustic modes propagating on the upper and lower surfaces: plate modes (Lamb modes) appear.
We have thus been able to predict that the presence of a phononic film on the plate causes the opening of a band gap for the antisymmetric A0 and symmetric S0 Lamb modes (Figure 2).
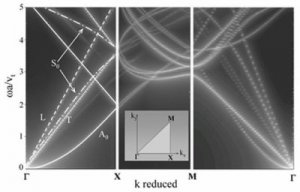
Figure 2: dispersion curves for a Fe/Cu phononic film on a thin silicon plate. The filling ratio is f = 0.564.
Experimental aspects
Our experimental setup has the great advantage of allowing measurements at any point inside the phononic crystal. We can thus record an image of the vibratory state of the whole system at each instant. It allowed us to demonstrate the creation of a gap in the spectrum of an elastic surface wave as it progresses in the phononic film.
This result constitutes the first experimental proof of the existence of a band gap in these systems (Figure 3).
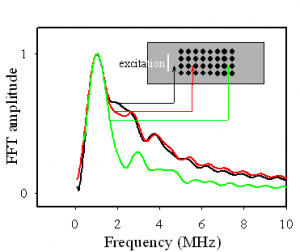
Figure 3: Fourier transforms of a surface wave recorded at three different locations during its propagation. The excitation of the ultrasonic pulse is done outside the phononic crystal. This one is a periodic array (1 mm pitch in both directions of the propagation plane) of 20 µm deep holes in a copper substrate.
We have also recently obtained original results concerning the measurement of the dispersion curves of a thin plate covered with a phononic film. For this purpose, an image of the vibratory state of the whole crystal at different times is recorded at different regularly spaced points. The two-dimensional Fourier transform of this image is the dispersion curve of the system (Figure 4).
We were able to highlight experimentally the band gap for the symmetrical Lamb mode S0 which appears around a frequency in very good agreement with that predicted by the theoretical model described above.
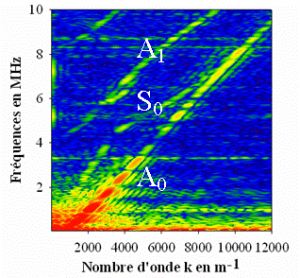
Figure 4: dispersion curves measured in a heterostructure made of a thin Fe/Cu phononic film deposited on a silicon plate. The filling ratio is f = 0.25.
On both sides of the band gap, the dispersion curves show a very strong curvature (see figures 1 and 2), as a consequence of the very strong frequency dispersion of the phase velocity of the wave. These properties, associated with the anisotropy of the system, give rise to very spectacular phenomena such as frequency selective focusing or an abnormal crossing speed of the phononic crystal.
Our experimental set-up allows us to measure the arrival time of an ultrasonic wave at any point of the surface of the same sample. We have observed that the periodicity of the inclusions induces an anomaly on the propagation speed of the surface wave, which translates into a crossing time of the crystal independent of the number of elementary cells in the path (Figure 5).
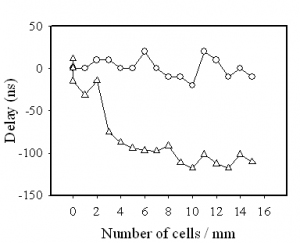
Figure 5: deviation from a reference time, of the transit time of an ultrasonic surface pulse as a function of the number of elementary cells crossed by the wave (triangles). For comparison, we show on the same figure the deviation measured in a sample where the inclusions are randomly distributed, but with the same filling rate (circles).

