List of members |
Facilities |
Internships and jobs |
PhD |
Publications |
News |
Team
- Permanent members: Fabio Finocchi, Simon Huppert
- Emeritus researcher: Philippe Depondt
Although the limits of classical statistical mechanics have been known for more than a century, in simulations, nuclei are almost invariably treated as classical particles. This is often inadequate to describe several properties (specific heat, phase transitions, isotopic effects, tunnel diffusion, etc…) especially for systems containing light elements or at low temperature: the wavelength of a hydrogen nucleus at ambient is close to interatomic distances. However, dealing precisely with nuclei quantum effects is very complex and simplified approaches are necessary. We have improved a semi-classical method, the quantum thermal bath (QTB), in which classical particles are in contact with a stochastic bath of oscillators respecting the Bose-Einstein statistic rather than that of Boltzmann and we have defined the conditions in which this method allows to have correct statistics. The QTB was implemented in the open-source DFT Quantum Espresso suite, allowing simulations of real “all-quantum” systems. The QTB approach leads to the same conclusions as the heavier integral paths (IP) method on the transition from pressurised ice towards phase X; it describes the evolution of the vibration spectra during the transition in very good agreement with the IR and Raman experiments, difficult to reach by the IPs. Its relative lightness makes it possible to tackle complex systems where the role of nuclear quantum effects is subtle. An example is provided by the insertion of 2% saline impurities in ice, which is sufficient to increase the transition to phase X by more than 20 GPa by the effect of the induced electric field.
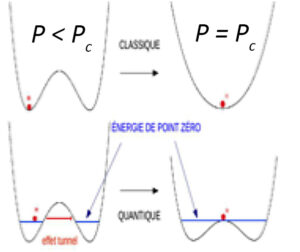
Figure: Quantum phase transition in pressurised ice. At high pressure, each H, linked by a covalent bond and a hydrogen bond (O-H… O), goes to a centro-symmetrical structure O—H—O, in phase X of ice. The free energy of the proton has two wells: classically, the barrier disappears at the critical pressure Pc(~ 100GPa), while from a quantum point of view the transition takes place when the zero-point energy is equal to the barrier (Pc~ 65 GPa).
Publications
- Yael Bronstein, Philippe Depondt, Fabio Finocchi, Antonino Marco Saitta. Quantum-driven phase transition in ice described via an efficient Langevin approach. Physical Review B: Condensed Matter and Materials Physics (1998-2015), American Physical Society, 2014, 89, pp.214101. ⟨10.1103/PhysRevB.89.214101⟩. ⟨hal-01003512⟩
- Yael Bronstein, Ph Depondt, Livia E Bove, Richard Gaal, A.Marco Saitta, et al.. Quantum versus classical protons in pure and salty ice under pressure. Physical Review B: Condensed Matter and Materials Physics (1998-2015), American Physical Society, 2016, 93, pp.024104. ⟨10.1103/PhysRevB.93.024104⟩. ⟨hal-01405481⟩

