When X-rays reveal the intimate deformations of lamellar materials
In our environment, we find many types of lamellar materials, from lamellar polymers to superimposed biological membranes and smectic liquid crystal materials. They are all governed by the same free energy expression, which generally avoids any expansion or contraction of the lamellar layers with respect to their equilibrium interlayer distance.
Scientists at INSP have deformed smectic liquid crystals into a cylindrical geometry in which the layers rotate through 90°. They measured the inter-layer distance as a function of the rotation angle on the SIXS line of the Soleil synchrotron. The team showed that layers closer to the center of curvature, characterized by a small radius of curvature, expand relative to flat layers. In collaboration with colleagues from the University of Pennsylvania in the USA, they showed that the phenomenological free energy usually used to interpret this observation must be modified. The scientists predict a dilation that increases with the inverse square of the radius of curvature, in perfect agreement with the experimental results.
This result suggests that this dilation is a general phenomenon that could affect many properties of the most deformed lamellar layers, including biological ones.
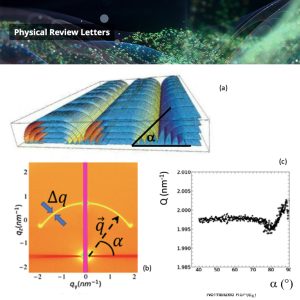
Caption: a) Schematic model of smectic layers stacked to form a network of hemicylinders (b) Diffusion of deformed smectic layers within hemicylinders with a being the angle of the normal to the layers with respect to the substrate. The smectic layers rotate through 90° so that the inter-layer distance (d) can be tracked as a varies by measuring q, the transfer vector (q = 2π/d) (c) Measuring q (and therefore d) as a varies between 40° and 90°. It can be seen that Q is smaller when the layers rotate (a between 40° and 85°) than when they are flat (a= 90°), so d is larger, and there is expansion of the rotating layers.
Reference
“X-Ray Diffraction Reveals the Consequences of Strong Deformation in Thin Smectic Films: Dilation and Chevron Formation”
Niyonzima, JD; Jeridi, H; Essaoui, L; Tosarelli, C; Vlad, A; Coati, A; Royer, S; Trimaille, I. Goldmann, M; Gallas, B; Constantin, D; Babonneau, D; Garreau, Y; Croset, B; Kralj, S; Kamien, RD; Lacaze, E.
Physical Review Letters, 2025

