Controlling the Winding Number of Topological Defects through Materials Engineering
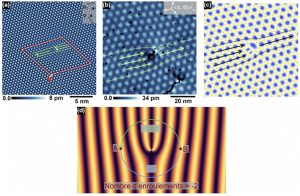Certain topological defects manifest as singularities or «nodes» in a phase field and are characterized by a winding number. A edge dislocation, is a typical example of such a defect, observed across a range of condensed matter systems including liquid crystals, atomic lattices, and magnetic textures. These defects are currently experiencing renewed interest due to their potential applications. In particular, their presence in topological materials could serve as hosts for non-Abelian anyons—quasiparticles of great interest for fault-tolerant quantum computing. In an experimental study using scanning tunneling microscopy, researchers at INSP, in collaboration with colleagues from IPCMS and the University of Liège, demonstrate that in a moiré superlattice formed between two epitaxially grown materials, a dislocation in one of the atomic lattices induces a corresponding dislocation in the moiré pattern. The winding number of the resulting dislocation in the moiré pattern subtly depends on the structural parameters of the two constituent materials. Using a simple mathematical model, the researchers show that the winding number of such topological defects can be tuned through careful material engineering.
Reference
“Higher Order Topological Defects in a Moiré Lattice”
Eugenio Gambari, Sebastian Meyer, Sacha Guesne, Pascal David, François Debontridder, Laurent Limot, Fabrice Scheurer, Christophe Brun, Bertrand Dupé, Tristan Cren, Marie Hervé.
Advanced functional materials, 34, 2407438 (2024)
Contact
Marie Hervé : marie.herve(at)insp.jussieu.fr
Caption: (a) Topography obtained by scanning tunneling microscopy showing that a dislocation with a winding number of 1 in the atomic lattice of CrCl₃ results in a dislocation with a winding number of –2 in the moiré lattice (b). (c) Numerical simulation of the moiré dislocation reproducing the experimental observations. (d) Analytical calculation of the winding number of the dislocation in the moiré pattern.
