List of members |
Facilities |
Internships and jobs |
PhD |
Publications |
News |
Equipe
- Permanent members: Martino Trassinelli, Christophe Prigent, Emily Lamour, Sébastien Steydli, Dominique Vernhet
Quantum Electrodynamics (QED) is regarded as the most tested quantum field theory. However, some discrepancies remain. New tests are needed, particularly in the regime of extreme fields like in heavy ions. Recently, we performed a high-precision measurement based on X-ray spectroscopy of helium-like uranium. For the first time, high-order non-perturbative predictions of quantum electrodynamics could be confirmed in this regime.
X-ray spectroscopy of helium-like uranium
To test quantum electrodynamics in extreme regimes, we conducted an experiment on helium-like uranium (U⁹⁰⁺), an ion containing only two electrons. The goal was to measure the 2p3/2 → 2s1/2 transition with unprecedented precision. This intra-shell transition, emitting photons of a few keV, is practically impossible to observe in hydrogen-like ions. Unlike n=2→1 transitions, it is accessible via Bragg reflection spectroscopy, a century-old method still offering remarkable resolution.
To produce these ions, uranium atoms were accelerated to near-light speeds at the GSI/FAIR Institute in Germany. They were then passed through a thin metal foil to strip them of nearly all their electrons. The resulting ions were stored in a storage ring, the ESR, where an extreme vacuum limits residual collisions. The desired transition was then obtained by making capturing an electron from hydrogen-like ions (with a single electron) by interacting with a supersonic gas jet target.
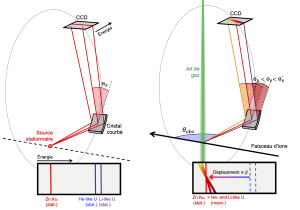
Figure 1 : Operation of a Bragg spectrometer for stationary sources (left) and moving sources (right). In the case of stationary sources, photons with different energies correspond to different Bragg angles, which are visualized by a position detector (e.g., an X-ray sensitive CCD camera) as spectral lines at different positions, as shown in the bottom frame. For fast ions, atomic transitions are induced by electron capture of the ions with a gas jet. Due to the Doppler effect, the energy of the photons in the laboratory frame depends on the ion speed (v = βc) and the observation angle θobs, which is close to 90°. Because of the finite extension, the crystal “sees” a finite range of observation angles, which correspond to slightly different energies and thus different Bragg angles, causing the spectral line to appear tilted. In our case, we use the Kα transition of zinc as a stationary calibration and a spectrometer with a Johan geometry featuring a curved germanium (220) crystal with a curvature radius R. In this geometry, the position detector must be placed near the Rowland circle (thin line in the figures), the circle tangent to the crystal with a diameter equal to R.
Bragg spectroscopy coupled with fast ion storage: a record precision
The key to this experiment lies in the use of a pair of Bragg spectrometers equipped with a curved germanium crystal and the clever exploitation of the Doppler effect. Bragg spectroscopy is a technique that allows measuring the energy of emitted photons with exceptional resolution. However, a major challenge is the systematic effects related to the Doppler effect, due to the uncertainty in the position of the supersonic jet relative to the spectrometers, specifically the observation angle θobs, and the high speed of the ions. To overcome this difficulties, the speed of the ions was adjusted so that the transitions of helium-like uranium and those of the reference ions (lithium-like U⁸⁹⁺ and beryllium-like U⁸⁸⁺) appear at the same energy in the laboratory frame. A stationary zinc source was also used and compared to the emission of the moving reference ions to calibrate the observation angle with a precision of 0.01°. Then, by comparing the transitions of the moving reference ions with that of helium-like uranium, the residual systematic error of the Doppler effect was then reduced by a factor proportional to the inverse of the difference between the ion velocities.
Thanks to this approach, the energy of the 2p3/2 → 2s1/2 transition was measured with an uncertainty of only 37 parts per million (ppm), or 0.17 eV on an energy of 4,510 eV. This precision allowed confirming for the first time the non-perturbative higher-order predictions of QED in a heavy ion with two electrons. It also enabled disentanble and separately testing the contributions of one- and two-electron effects.
Figure 2 : Left: Comparison of the presented measurement with past experiments and various theoretical predictions. Right: Comparison of the experimental uncertainty with different contributions of quantum electrodynamics for one electron (orders α and α²) and two electrons corresponding to the exchange of one photon (“Breit approx. for 2 el.”), two photons (“Non-radiative QED for 2 el.”), and mixed diagrams of photon exchange and self-energy or vacuum polarization (“Non-radiative QED for 2 el.”).
Towards even greater precision
Although this experiment represents a major advance, current theoretical uncertainties remain limited by approximate calculations of the α² order terms and by the imperfect knowledge of nuclear structure. A new experiment is already in preparation to achieve a precision of 2 ppm, using a lighter reference transition, such as that of scandium, where QED effects are negligible. More details can be found in the new project description.
Collaborations
- Groupe de physique atomique du GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Allemagne
- Institut für Optik und Quantenelektronik, Friedrich-Schiller-Universität, Jena, Allemagne
- Équipe de métrologie du Laboratoire Kastler Brossel, Paris, France
- Institute of Physics, Jan Kochanowski University, Kielce, Pologne
- Department of Physics, NOVA University Lisbon, Caparica, Portugal
Publications
-
[Loetzsch2024] R. Loetzsch, H. F. Beyer, L. Duval, U. Spillmann, … M. Trassinelli, Testing Quantum Electrodynamics in Extreme Fields Using Helium-like Uranium, Nature, 2024, 625 (7996), pp. 673–678. ⟨10.1038/s41586-023-06910-y⟩⟨hal-04419190⟩
-
[Trassinelli2023] M. Trassinelli, Shape and Satellite Studies of Highly Charged Ions X-ray Spectra Using Bayesian Methods, Atoms, 2023, 11 (4), pp. 64. ⟨10.3390/atoms11040064⟩⟨hal-04297402⟩
