Liste des membres |
Equipements |
Stages et Emplois |
Thèses |
Publications |
Actualités |
Equipe
- Membres permanents : Olga Boyko
- Chercheur émérite : Bernard Bonello
Aspects théoriques
A l’instar de ce qu’il s’est passé il y a une vingtaine d’années pour les cristaux photoniques, on assiste à l’heure actuelle à une certaine effervescence autour des cristaux phononiques qui, en principe, doivent présenter pour les ondes acoustiques les mêmes propriétés de filtrage, de guidage, de focalisation, de localisation… que celles observées pour les ondes électromagnétiques dans les cristaux photoniques.
Jusqu’à présent, la grande majorité des travaux consacrés à ces systèmes concernent la propagation d’ondes élastiques de volume dans des structures périodiques où l’un des constituants est un fluide (l’air en général). Les déplacements transversaux ne sont donc jamais pris en considération. Ce n’est que depuis peu que les ondes de surface font l’objet d’une attention particulière. Une partie importante de notre activité concerne le calcul des courbes de dispersion de systèmes phononiques proches de ceux que nous étudions expérimentalement (voir plus bas). Ceux-ci sont ce qu’on pourrait appeler des « films phononiques » c’est-à-dire des structures constituées d’inclusions périodiques de symétrie carrée d’un matériau A, dans un film mince d’un matériau B, lui-même déposé à la surface d’un substrat homogène semi-infini d’un matériau C.
Si l’épaisseur du film est inférieure à la distance de répétition des inclusions, l’onde élastique se propage en partie dans le film et en partie dans le substrat et il n’y a donc a priori aucune évidence qu’une bande interdite apparaisse pour l’onde de surface. Nous avons néanmoins montré qu’il y a apparition d’une bande interdite et repliement pour le mode de surface, au bord X de la mini zone de Brillouin, pour la configuration film mince phononique sur substrat homogène semi-infini (Figure 1). Le gap s’étend partiellement dans la partie XM de la zone de Brillouin.

Figure 1 : courbes de dispersion dans la direction GX, pour d’un film phononique constitué d’inclusions cylindriques de fer dans un film mince de cuivre, déposé sur un substrat de silicium. Le taux de remplissage est f = 0,564. Le pas du réseau carré est 2 fois l’épaisseur du film. Tlay, Tsub et Lsub font référence respectivement aux modes transverse dans le film, transverse dans le substrat et longitudinal dans le substrat. L’insert est un grossissement mettant en évidence la bande interdite et le repliement du mode de Rayleigh en bord de zone.
Nous nous intéressons également à une configuration dans laquelle le substrat homogène a une épaisseur finie. Le système est alors une plaque sur laquelle est déposé le film phononique. Dans ce cas, il y a couplage entre les modes acoustiques qui se propagent sur les faces supérieure et inférieure : des modes de plaque (modes de Lamb) apparaissent.
Nous avons ainsi pu prévoir que la présence d’un film phononique sur la plaque provoquait l’ouverture d’une bande interdite pour les modes de Lamb antisymétrique A0 et symétrique S0 (Figure 2).
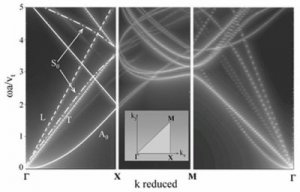
Figure 2 : courbes de dispersion pour un film phononique Fe/Cu sur une plaque mince de silicium. Le taux de remplissage est f = 0,564.
Aspects expérimentaux
Notre montage expérimental présente le très grand avantage d’autoriser des mesures en n’importe quel point à l’intérieur du cristal phononique. On peut ainsi enregistrer une image de l’état vibratoire de l’ensemble du système à chaque instant. Il nous a permis de mettre en évidence le creusement d’un gap dans le spectre d’une onde élastique de surface au fur et à mesure qu’elle progressait dans le film phononique.
Ce résultat constitue la première preuve expérimentale de l’existence d’une bande interdite dans ces systèmes (Figure 3).
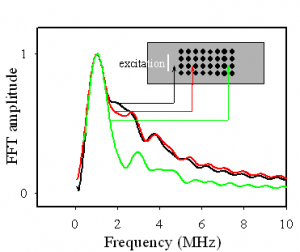
Figure 3 : Transformées de Fourier d’une onde de surface enregistrées en trois endroits différents, au cours de sa propagation. L’excitation de l’impulsion ultrasonore se fait à l’extérieur du cristal phononique. Celui-ci est un réseau périodique (pas de 1 mm dans les 2 directions du plan de propagation) de trous de 20 µm de profondeur dans un substrat de cuivre.
Nous avons également obtenu récemment des résultats originaux concernant la mesure des courbes de dispersion d’une plaque mince recouverte d’un film phononique. Pour cela, on enregistre en différents points régulièrement espacés, une image de l’état vibratoire de l’ensemble du cristal à différents instants. La transformée de Fourrier bi-dimensionnelle de cette image est la courbe de dispersion du système (Figure 4).
Nous avons ainsi pu mettre en évidence expérimentalement la bande interdite pour le mode de Lamb symétrique S0 qui apparaît autour d’une fréquence en très bon accord avec celle prévue par le modèle théorique que décrit plus haut.
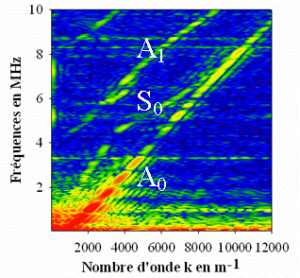
Figure 4 : courbes de dispersion mesurées dans une hétérostructure constituée d’un film mince phononique Fe/Cu déposée sur une plaque de silicium. Le taux de remplissage est f = 0,25.
De part et d’autre de la bande interdite, les courbes de dispersion présentent une très forte courbure (voir les figures 1 et 2), conséquence de la très forte dispersion en fréquence de la vitesse de phase de l’onde. Ces propriétés, associée à l’anisotropie du système, donnent lieu à des phénomènes très spectaculaires comme la focalisation sélective en fréquence ou une vitesse de traversée anormale du cristal phononique.
Notre montage expérimental nous permettant de mesurer le temps d’arrivée d’une onde ultrasonore en n’importe quel point de la surface d’un même échantillon, nous avons pu observer que la périodicité des inclusions induisait sur la vitesse de propagation de l’onde de surface, une anomalie qui se traduit par un temps de traversée du cristal indépendant du nombre de cellules élémentaires dans le chemin (Figure 5).
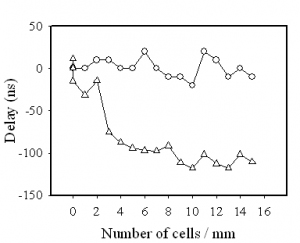
Figure 5 : écart par rapport à un temps de référence, du temps de transit d’une impulsion ultrasonore de surface en fonction du nombre de cellules élémentaire traversée par l’onde (triangles). Pour comparaison, on porte sur la même figure l’écart mesuré dans un échantillon où les inclusions sont réparties aléatoirement, mais avec le même taux de remplissage (cercles).

