Oxydes en basses dimensions – Effets quantiques nucléaires dans les oxydes

Bien que les limites de la mécanique statistique classique soient connues depuis plus d’un siècle, dans les simulations, les noyaux sont presque invariablement assimilés à des particules classiques. Ceci est souvent inadéquat pour décrire plusieurs propriétés (chaleur spécifique, transitions de phase, effets isotopiques, diffusion tunnel…) surtout pour des systèmes contenant des éléments légers ou à basse température : la longueur d’onde d’un noyau H à l’ambiante est proche des distances interatomiques. Or, traiter exactement les effets quantiques sur les noyaux est très complexe et des approches simplifiées s’imposent. Nous avons amélioré une méthode semi-classique, le bain thermique quantique (QTB), dans laquelle des particules classiques sont en contact avec un bain stochastique d’oscillateurs respectant la statistique de Bose-Einstein plutôt que celle de Boltzmann et nous avons défini les conditions dans lesquelles cette méthode permet d’avoir des moyennes statistiques correctes. Le QTB a été installé dans la suite open-source DFT Quantum Espresso permettant ainsi des simulations de systèmes réels « tout-quantiques ». L’approche QTB aboutit aux mêmes conclusions que la méthode des intégrales de chemin (PI), plus lourde, sur la transition de la glace sous pression vers la phase X ; elle décrit l’évolution des spectres de vibration pendant la transition en très bon accord avec les expériences IR et Raman, difficilement atteignables par les PI. Sa relative légèreté permet de s’attaquer à des systèmes complexes où le rôle des effets quantiques nucléaires est subtil. Un exemple est fourni par l’insertion de 2 % d’impuretés salines dans la glace, qui suffit à augmenter de plus de 20 GPa la transition vers la phase X par l’effet du champ électrique induit. 

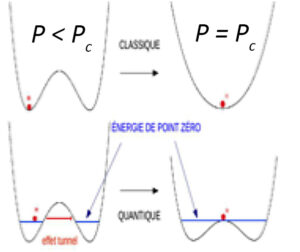
Figure : Transition de phase quantique dans la glace sous pression. A pression élevée, chaque H, lié par une liaison covalente et une liaison hydrogène (O-H…O), passe à une structure centro-symétrique O—H—O, dans la phase X. L’énergie libre du proton comporte deux puits : classiquement, la barrière disparaît à la pression critique Pc (~100GPa), tandis que du point de vue quantique la transition a lieu lorsque l’énergie de point zéro est égale à la barrière (Pc ~ 65 GPa).

Publications

• Yael Bronstein, Philippe Depondt, Fabio Finocchi, Antonino Marco Saitta. Quantum-driven phase transition in ice described via an efficient Langevin approach. Physical Review B: Condensed Matter and Materials Physics (1998-2015), American Physical Society, 2014, 89, pp.214101. ⟨10.1103/PhysRevB.89.214101⟩. ⟨hal-01003512⟩
  
• Yael Bronstein, Ph Depondt, Livia E Bove, Richard Gaal, A.Marco Saitta, et al.. Quantum versus classical protons in pure and salty ice under pressure. Physical Review B: Condensed Matter and Materials Physics (1998-2015), American Physical Society, 2016, 93, pp.024104. ⟨10.1103/PhysRevB.93.024104⟩. ⟨hal-01405481⟩